Hình trụ là một trong những hình học không gian thú vị và được ứng dụng nhiều trong đời sống hàng ngày. Vậy bạn đã thực sự hiểu được bản chất và các công thức tính liên quan tới hình học quen thuộc này chưa? Cùng HOCMAI tìm hiểu trong bài viết dưới đây
I. Khái niệm hình trụ
Hình trụ là một hình học không gian (3D), là hình được giới hạn bởi hai đường tròn có đường kính bằng nhau và mặt trụ.
Theo định nghĩa sách giáo khoa Toán lớp 9, hình trụ là là:
“Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.”
“Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.”
Theo một cách dễ hiểu hơn, ta sẽ có một hình trụ khi xoay một hình chữ nhật ABCD theo một cạnh cố định (Cạnh AB theo ví dụ dưới đây):
Để có thể nhận biết hình trụ một cách dễ dàng, bạn có thể dựa vào một số tính chất sau:
- Hình trụ có hai mặt đáy là hình tròn và đường kính bằng nhau
- Hai cạnh có độ dài bằng nhau khi chúng song song với nhau
- Đường thẳng nối từ hai tâm của hai mặt đáy chính là trục tọa độ của hình trụ.
- Các đường thẳng có cùng độ dài và song song với trục tọa độ được gọi là các đường sinh của hình trụ.
II. Công thức và cách tính Diện tích hình trụ
Diện tích hình trụ bao gồm diện tích xung quanh và diện tích toàn phần của nó. Sau đây là công thức và cách tính cụ thể từng loại diện tích hình trụ HOCMAI gửi đến bạn.
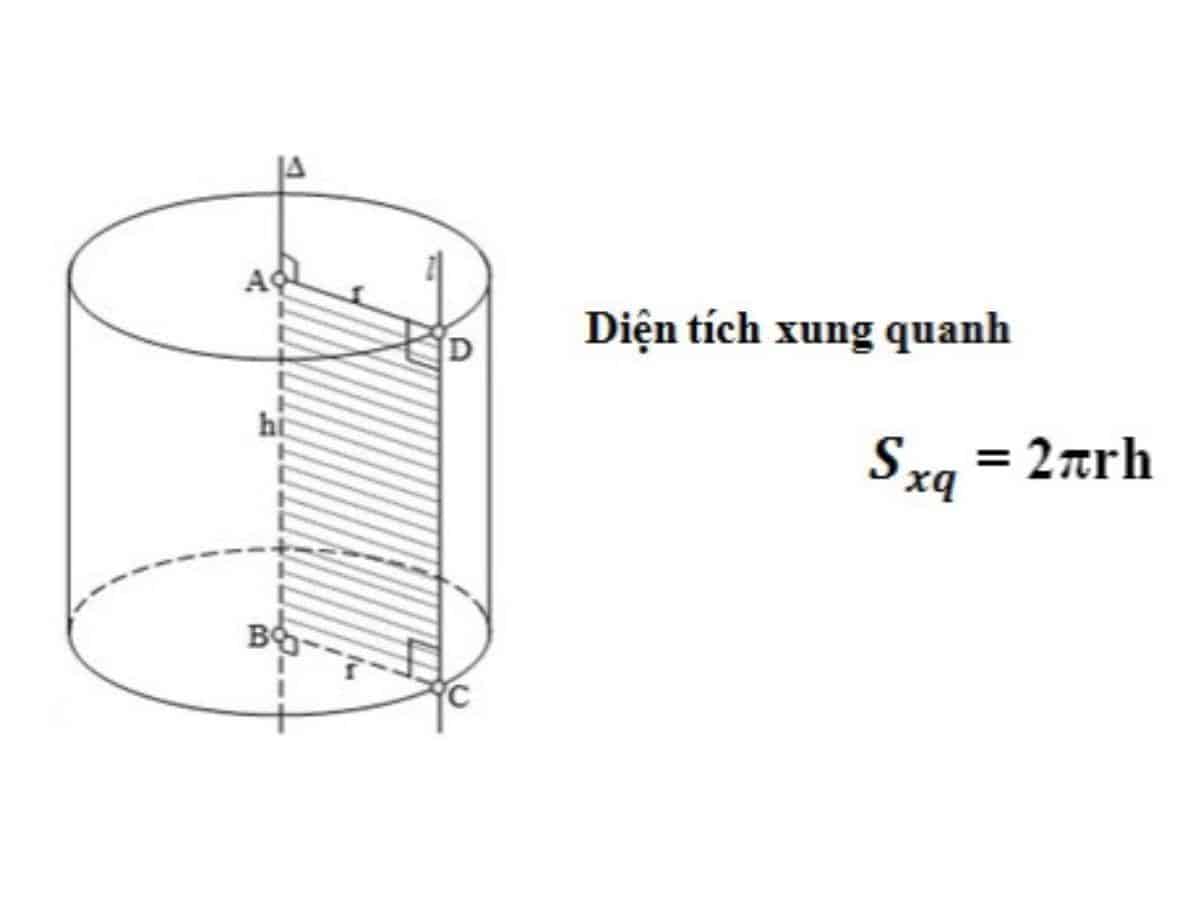
1. Diện tích xung quanh hình trụ
Diện tích xung quanh chỉ phần diện tích mặt bao quanh của hình trụ, không bao gồm diện tích của 2 đáy.
Để tính được diện tích xung quanh hình trụ, chúng ta sẽ lấy chu vi đường tròn đáy nhân với chiều cao. Công thức cụ thể là:
Sxq = 2.π.r.h
Trong đó:
- Sxq là diện tích xung quanh hình trụ
- 2πr là chu vi đường tròn đáy (với π = 3,14)
- h là chiều cao của hình trụ
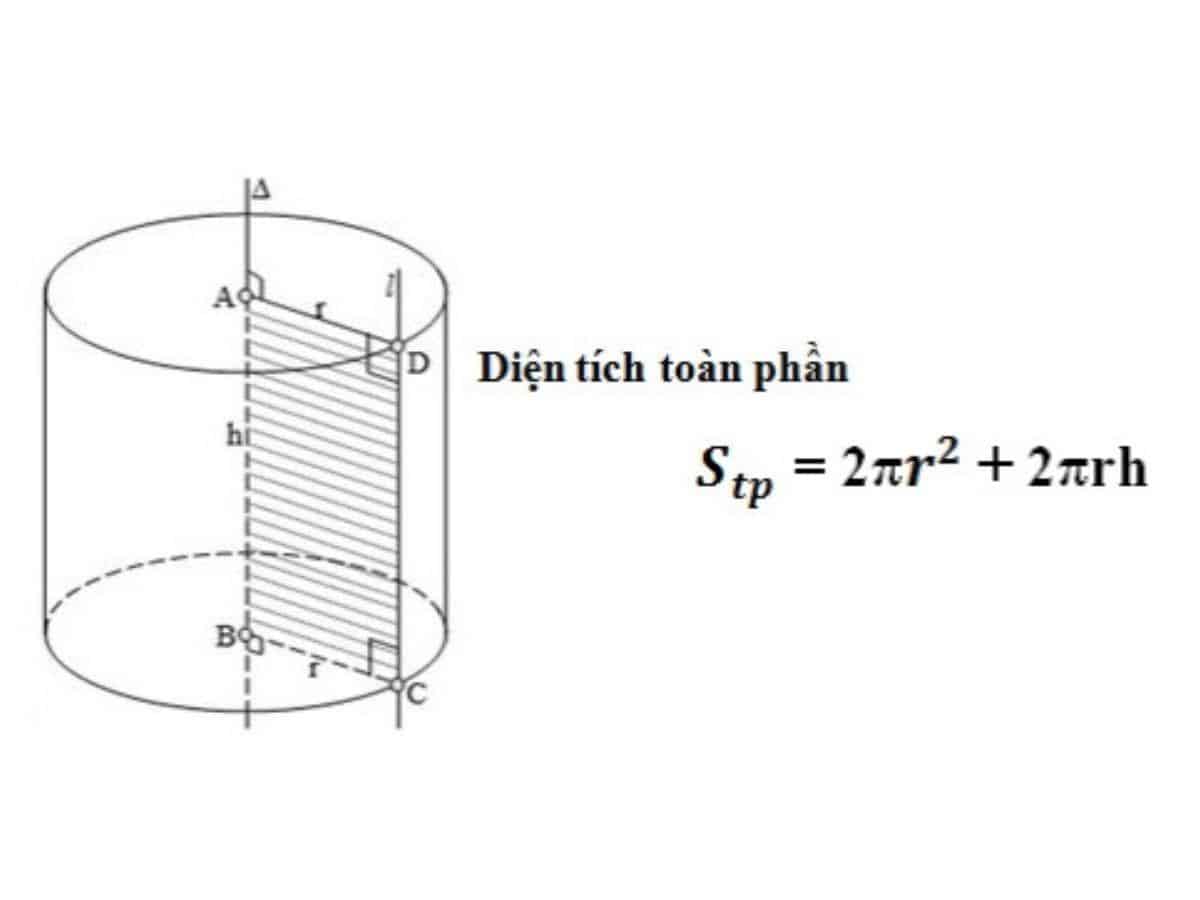
2. Diện tích toàn phần hình trụ
Diện tích toàn phần của hình trụ bao gồm phần diện tích bao quanh và diện tích đáy của hình trụ.
Để tính được diện tích toàn phần hình trụ, chúng ta sẽ lấy diện tích xung quanh hình trụ cộng với diện tích của 2 đáy. Công thức cụ thể là:
Stp = 2.π.r² + 2.π.r.h
Trong đó:
- Stp là diện tích toàn phần hình đáy
- 2πr^2 diện tích của 2 đường tròn đáy (với π = 3,14)
- 2πrh là diện tích xung quanh hình đáy
3. Ví dụ về tính toán diện tích xung quanh và diện tích toàn phần hình trụ
Bài tập: Cho một hình trụ có r = 5 cm, h = 10 cm. Hãy tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Hướng dẫn giải
Diện tích xung quanh hình trụ là:
Sxq = 2 * π * r * h = 2 * π * 5 * 10 = ~ 314 (cm2)
Diện tích toàn phần hình trụ là:
Stp = 2 * π * r ^2* + Sxq = 2 * π * 5^2 + 314= ~ 471 cm2
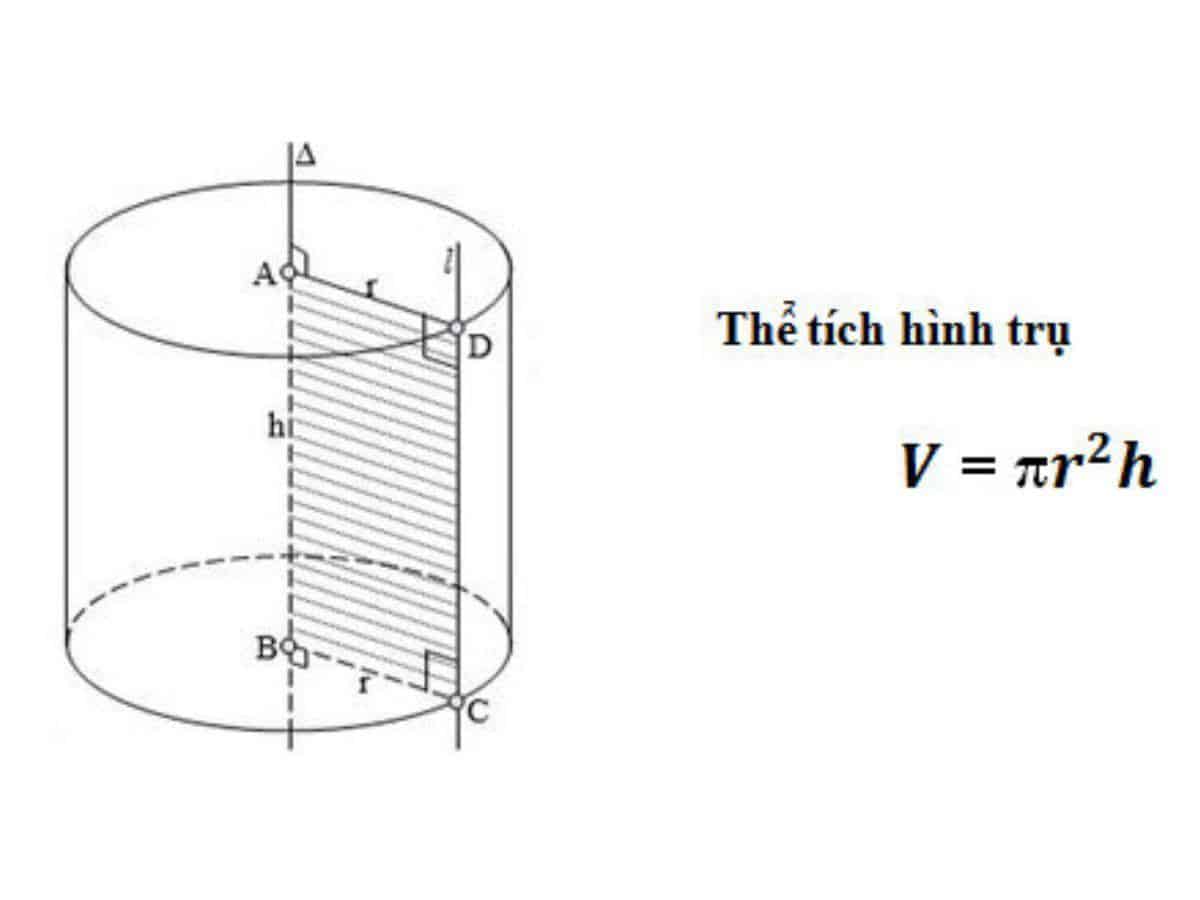
III. Thể tích và cách tính thể tích hình trụ
Thể tích hình trụ là lượng không gian mà hình trụ ấy chiếm. Để tính được thể tích hình trụ, bạn cần sử dụng đơn vị đo lập phương của khoảng cách (mũ 3 khoảng cách).
1. Công thức tính thể tích hình trụ
Thể tích hình trụ là lượng không gian được chiếm giữ một hình trụ nhất định. Để tính được thể tích hình trụ, bạn cần lấy diện tích đáy nhân cho chiều cao của hình trụ. Cụ thể là:
V = π.r².h
Trong đó:
- V là thể tích hình trụ
- πr² là diện tích đáy
- h là chiều cao
2. Ví dụ về tính toán thể tích hình trụ
Bài tập: Cho một hình trụ có r = 5 cm, h = 10 cm. Hãy tính thể tích của hình trụ.
Hướng dẫn giải
Thể tích hình trụ là:
V = π * r ^2 * h = π * 5^2 * 10 = ~ 785 (cm3)
III. Những ứng dụng của hình trụ trong đời sống
Theo các chuyên gia, hình trụ có nhiều đặc tính vượt trội như khả năng chịu lực tốt, khả năng lưu trữ không gian tốt hơn so với những hình dạng thường gặp là hình khối hộp hay hình cầu. Bởi vậy trong cuộc sống hằng ngày, bạn sẽ bắt gặp khá nhiều ứng dụng của hình trụ. Trong đó những lon nước ngọt có thiết kế hình trụ chính là ứng dụng bạn thường gặp nhất.
Nhờ khả năng chịu lực vô cùng tốt, hình trụ được mô phỏng qua nhiều hình dạng cấu trúc như ống khói, đường ống nước, cột trụ,…
Một số bài viết bạn có thể quan tâm:
Cách tính diện tích hình tròn, chu vi hình tròn
Diện tích hình bình hành, chu vi hình bình hành
Cách tính diện tích hình thang, chu vi hình thang
HOCMAI hy vọng bài này sẽ giúp các bạn học sinh hiểu rõ về hình trụ cùng các kiến thức liên quan tới hình học không gian thú vị này. Truy cập hoctot.hocmai.vn để tham khảo thêm những kiến thức toán học tương tự và không bỏ lỡ những bài viết mới nhất của chúng tớ nhé!