Các thuật toán dựa trên cây được sử dụng để truy cập từng nút hoặc đỉnh trong đồ thị. Chúng ta có thể truy cập từng nút trong đồ thị bằng cách lặp qua tất cả các nút của đồ thị bằng cách sử dụng thuật toán trên từng nút chưa được duyệt. Hai thuật toán thường được sử dụng để duyệt đồ thị là tìm kiếm theo chiều rộng (BFS) và tìm kiếm theo chiều sâu (DFS), nhưng ở đây chúng ta hiểu là tìm kiếm theo chiều rộng. Tìm kiếm theo chiều rộng (BFS) được sử dụng để giải quyết nhiều vấn đề, bao gồm tìm đường đi ngắn nhất trong biểu đồ hoặc giải các trò chơi giải đố như Khối Rubik.
1. BFS là gì?
Tìm kiếm theo chiều rộng (BFS) là một thuật toán để duyệt đồ thị hoặc cây. BFS áp dụng cho cây và đồ thị gần như giống nhau. Sự khác biệt duy nhất là đồ thị có thể chứa các chu trình, vì vậy chúng ta có thể duyệt lại cùng một nút. Để tránh xử lý lại cùng một nút, chúng ta sử dụng mảng boolean đã truy cập, mảng này sẽ đánh dấu các đỉnh đã truy cập. BFS sử dụng cấu trúc dữ liệu hàng đợi (queue) để tìm đường đi ngắn nhất trong biểu đồ.
2. Thuật toán BFS
triển khai BFS tiêu chuẩn sẽ đặt mỗi đỉnh của đồ thị vào một trong hai loại: visited, not visited. Mục đích của thuật toán là đánh dấu mỗi đỉnh là đã thăm để tránh các chu trình.
Cách thuật toán hoạt động như sau:
- Lấy một đỉnh bất kỳ trong đồ thị thêm vào cuối hàng đợi.
- Lấy phân tử đầu tiên của hàng đợi và thêm nó vào danh sách đã duyệt.
- Tạo một danh sách các đỉnh liền kề của đỉnh đang xét. Thêm những đỉnh không có trong danh sách đã duyệt vào cuối hàng đợi.
- Tiếp tục lặp lại bước 2 và 3 cho đến khi hàng đợi trống.
Lưu ý: Đồ thị có thể chứa hai thành phần không liên kết khác nhau, vì vậy để đảm bảo rằng mọi đỉnh đều đã được thăm, chúng ta cũng có thể chạy thuật toán BFS trên mọi đỉnh.
3. Ví dụ về BFS
Hãy xem cách hoạt động của thuật toán Tìm kiếm theo chiều rộng với một ví dụ. Ta dùng đồ thị vô hướng có 5 đỉnh. 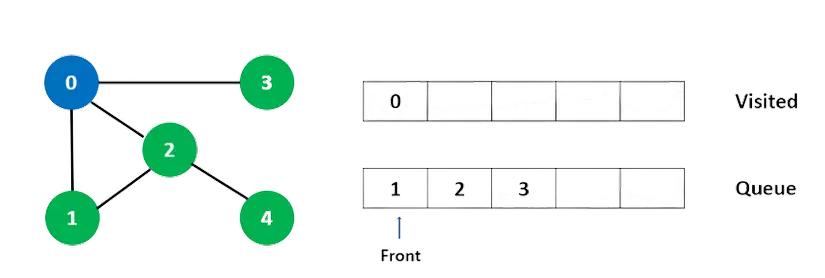 Chúng ta bắt đầu từ đỉnh 0, thuật toán BFS bắt đầu bằng cách đặt nó vào danh sách đã duyệt và đặt tất cả các đỉnh liền kề của nó vào hàng đợi. Tiếp theo, chúng tôi truy cập phần tử đầu của hàng đợi, tức là 1 và đi đến các nút liền kề của nó. Vì 0 đã được truy cập, thay vào đó, chúng tôi truy cập 2.
Chúng ta bắt đầu từ đỉnh 0, thuật toán BFS bắt đầu bằng cách đặt nó vào danh sách đã duyệt và đặt tất cả các đỉnh liền kề của nó vào hàng đợi. Tiếp theo, chúng tôi truy cập phần tử đầu của hàng đợi, tức là 1 và đi đến các nút liền kề của nó. Vì 0 đã được truy cập, thay vào đó, chúng tôi truy cập 2.  Đỉnh 2 có một đỉnh liền kề chưa được thăm là 4, vì vậy chúng tôi thêm đỉnh đó vào cuối hàng đợi và thăm 3, ở đầu hàng đợi.
Đỉnh 2 có một đỉnh liền kề chưa được thăm là 4, vì vậy chúng tôi thêm đỉnh đó vào cuối hàng đợi và thăm 3, ở đầu hàng đợi. 
 Chỉ còn lại 4 trong hàng đợi vì nút liền kề duy nhất của 3 tức là 0 đã được truy cập. Chúng ta đến thăm nó. Vì hàng đợi trống, chúng ta đã hoàn thành việc tìm kiếm theo chiều rộng trên đồ thị.
Chỉ còn lại 4 trong hàng đợi vì nút liền kề duy nhất của 3 tức là 0 đã được truy cập. Chúng ta đến thăm nó. Vì hàng đợi trống, chúng ta đã hoàn thành việc tìm kiếm theo chiều rộng trên đồ thị.
4. Cài đặt BFS
// BFS algorithm in Java import java.util.*; public class Graph { private int V; private LinkedList<Integer> adj[]; // Create a graph Graph(int v) { V = v; adj = new LinkedList[v]; for (int i = 0; i < v; ++i) adj[i] = new LinkedList(); } // Add edges to the graph void addEdge(int v, int w) { adj[v].add(w); } // BFS algorithm void BFS(int s) { boolean visited[] = new boolean[V]; LinkedList<Integer> queue = new LinkedList(); visited[s] = true; queue.add(s); while (queue.size() != 0) { s = queue.poll(); System.out.print(s + ” “); Iterator<Integer> i = adj[s].listIterator(); while (i.hasNext()) { int n = i.next(); if (!visited[n]) { visited[n] = true; queue.add(n); } } } } public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3); System.out.println(“Following is Breadth First Traversal ” + “(starting from vertex 2)”); g.BFS(2); } }
5. Độ phức tạp của BFS
Độ phức tạp thời gian của thuật toán BFS được biểu diễn dưới dạng O(V + E), trong đó V là số nút và E là số cạnh.
Độ phức tạp không gian của thuật toán là O(V).
6. Ứng dụng của BFS
Tìm kiếm theo chiều rộng là một phương pháp duyệt đồ thị đơn giản có phạm vi ứng dụng cao. Một số ứng dụng của BFS:
- Trình thu thập dữ liệu trong Công cụ Tìm kiếm: Tìm kiếm theo chiều rộng là thuật toán chính được sử dụng để lập chỉ mục các trang web. Thuật toán BFS bắt đầu từ trang nguồn và đi theo tất cả các liên kết được liên kết với nó.
- Mạng peer-to-peer: Tìm kiếm theo chiều rộng có thể được sử dụng để tìm tất cả các nút lân cận trong mạng peer-to-peer. Ví dụ: BitTorrent sử dụng BFS để giao tiếp peer-to-peer.
- Hệ thống định vị GPS: Thuật toán tốt nhất để xác định đường đi ngắn nhất từ vị trí này đến vị trí khác là tìm kiếm theo chiều rộng.
- Thuật toán Ford-Fulkerson: Để tìm luồng cực đại trong mạng, hãy sử dụng thuật toán Ford-Fulkerson.
- Đường đi ngắn nhất & cây khung tối thiểu cho đồ thị không trọng số: Tìm kiếm theo chiều rộng được sử dụng để tìm đường đi ngắn nhất & cây khung tối thiểu cho đồ thị không trọng số.
7. Kết luận
- Tìm kiếm theo chiều rộng (BFS) được sử dụng để giải quyết nhiều vấn đề, bao gồm tìm đường đi ngắn nhất trong biểu đồ hoặc giải các trò chơi giải đố như Khối Rubik.
- BFS sử dụng cấu trúc dữ liệu hàng đợi để tìm đường đi ngắn nhất trong biểu đồ.
- Để tránh xử lý lại cùng một nút, chúng ta sử dụng mảng boolean đã duyệt, mảng này sẽ đánh dấu các đỉnh đã truy cập.
- Đồ thị có thể chứa hai thành phần không liên kết khác nhau, vì vậy để đảm bảo rằng mọi đỉnh đều đã được duyệt, chúng ta cũng có thể chạy thuật toán BFS trên mọi đỉnh.
- Độ phức tạp thời gian của thuật toán tìm kiếm theo chiều rộng là O(V+E) và độ phức tạp không gian là O(V).
Nguồn:
- https://www.programiz.com/dsa/graph-bfs
- https://www.scaler.com/topics/breadth-first-search-python/
